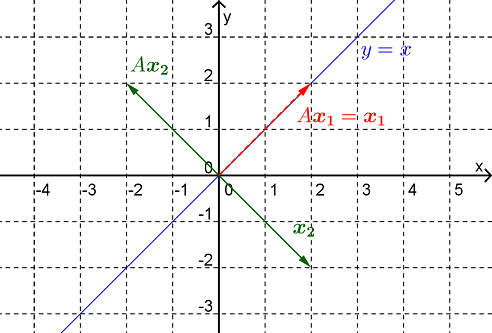
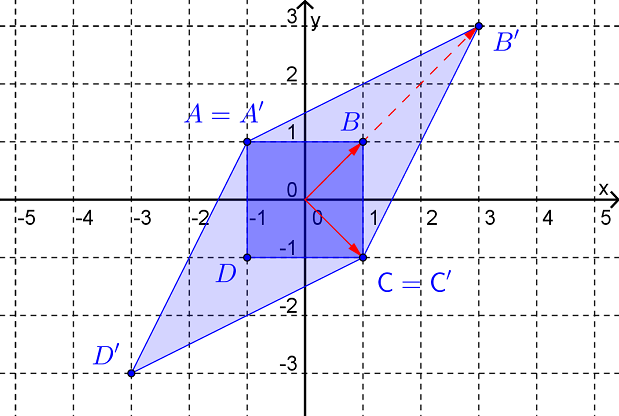
The characteristic equation for \(A\) is
\begin{equation*}
\det\begin{pmatrix} 7-\lambda \amp 1 \amp -2 \\ 0 \amp 3-\lambda \amp 6 \\ 0 \amp 0 \amp 2-\lambda \end{pmatrix}=0
\end{equation*}
Now, using the minors method and expanding down column 1,
\begin{align*}
\det\begin{pmatrix} 7-\lambda \amp 1 \amp -2 \\ 0 \amp 3-\lambda \amp 6 \\ 0 \amp 0\amp 2-\lambda \end{pmatrix} \amp =(7-\lambda)\begin{vmatrix} 3-\lambda \amp 6 \\ 0 \amp 2-\lambda \end{vmatrix}-0\begin{vmatrix} 1 \amp -2 \\ 0 \amp 2-\lambda \end{vmatrix}+0\begin{vmatrix} 1 \amp -2 \\ 3-\lambda \amp 6 \end{vmatrix} \\
\amp = (7-\lambda)\{(3-\lambda)(2-\lambda)-0\}-0+0\\
\amp = (7-\lambda)(3-\lambda)(2-\lambda)
\end{align*}
Thus the eigenvalues for \(A\) satisfy
\begin{equation*}
\lambda=2,3,7
\end{equation*}
When \(\lambda=2\) the augmented matrix and its reduced row echelon form are
\begin{equation*}
\begin{pmatrix} 5 \amp 1 \amp -2 \amp 0 \\ 0 \amp 1 \amp 6 \amp 0 \\ 0 \amp 0 \amp 0 \amp 0 \end{pmatrix} \sim \begin{pmatrix} 5 \amp 0 \amp -8 \amp 0 \\ 0 \amp 1 \amp 6 \amp 0 \\ 0 \amp 0 \amp 0 \amp 0 \end{pmatrix}
\end{equation*}
Thus, the eigenvectors take the form
\begin{align*}
\mathbf{x} \amp =\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \textrm{ where } \begin{matrix} \hspace{2mm} 5x_1-8x_3=0 \\ \hspace{4mm} x_2+6x_3=0 \end{matrix} \\
\Rightarrow \mathbf{x} \amp =\begin{pmatrix} 8t \\ -30t \\ 5t \end{pmatrix} = t\begin{pmatrix} 8 \\ -30 \\ 5 \end{pmatrix}
\end{align*}
When \(\lambda=3\) the augmented matrix and its reduced row echelon form are
\begin{equation*}
\begin{pmatrix} 4 \amp 1 \amp -2 \amp 0 \\ 0 \amp 0 \amp 6 \amp 0 \\ 0 \amp 0 \amp -1 \amp 0 \end{pmatrix} \sim \begin{pmatrix} 4 \amp 1 \amp 0 \amp 0 \\ 0 \amp 0 \amp 1 \amp 0 \\ 0 \amp 0 \amp 0 \amp 0 \end{pmatrix}
\end{equation*}
Thus, the eigenvectors take the form
\begin{align*}
\mathbf{x} \amp =\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \textrm{ where } \begin{matrix} \hspace{2mm} 4x_1+x_2=0 \\ \hspace{14.5mm} x_3=0 \end{matrix} \\
\Rightarrow \mathbf{x} \amp =\begin{pmatrix} -t \\ 4t \\ 0 \end{pmatrix} = t\begin{pmatrix} -1 \\ 4 \\ 0 \end{pmatrix}
\end{align*}
When \(\lambda=7\) the augmented matrix and its reduced row echelon form are
\begin{equation*}
\begin{pmatrix} 0 \amp 1 \amp -2 \amp 0 \\ 0 \amp -4 \amp 6 \amp 0 \\ 0 \amp 0 \amp -5 \amp 0 \end{pmatrix} \sim \begin{pmatrix} 0 \amp 1 \amp 0 \amp 0 \\ 0 \amp 0 \amp 1 \amp 0 \\ 0 \amp 0 \amp 0 \amp 0 \end{pmatrix}
\end{equation*}
Thus, the eigenvectors take the form
\begin{align*}
\mathbf{x} \amp =\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \textrm{ where } \begin{matrix} \hspace{2mm} x_2=0 \\ \hspace{2mm} x_3=0 \end{matrix} \\
\Rightarrow \mathbf{x} \amp =\begin{pmatrix} t \\ 0 \\ 0 \end{pmatrix} = t\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}
\end{align*}